Dolma Partisi

[English] [kod]
[Substack]

Geçenlerde dolma temalı yıllık bir akşam yemeği partisinin yirmi üçüncüsüne katıldım. Tahmin edebileceğiniz gibi bu etkinlik bazıları için bir gelenek haline gelmiş – ilki düzenlendiğinde ben sadece iki yaşındaydım. Kurallar gereği herkesin ev yapımı bir dolma getirmesi gerekiyordu, yalnız marketten alınan “ev yapımı” dolmalar sayılmıyor. Organizatörlerden gelen resmi bir duyuruda belirtildiği gibi, “ev yapımı dolmanız kendi ellerinizle yapılmış olmalı”.

Parti sırasında kayıt işlemlerine yardım ettim. Yeni gelenler dolmaları için benden bir etiket alıyorlardı. Her dolma için dört parametre vardı: “vegan”, “vejetaryen”, “kırmızı et yok” ve “süt ürünü yok”. Bu yazıyı yazma fikri bu etiketlerden çıktı.

Bu dört parametrenin $2^4 = 16$ kombinasyonunun içinde bazılarının mümkün olmadığını görmek zor değil. Bir dolma “vegan” ise zaten diğer üç sınıfın da içinde olmak zorunda, dolayısıyla hem kırmızı et içerip hem de vegan olan bir dolma olamaz. Eğer biri böyle bir dolma yapmayı başarırsa bu gerçekten büyük bir başarı olur. Peki hangi kombinasyonlar mümkün? Önce tüm olası kombinasyonları sıralayacağız, sonra da her kombinasyon için ya imkansız olduğunu göstereceğiz ya da o kombinasyonda olan bir dolmanın hangi malzemeleri içerebileceğini/içermesi gerektiğini listeleyeceğiz. Bunun için aşağıdaki Venn diyagramını çizdim:

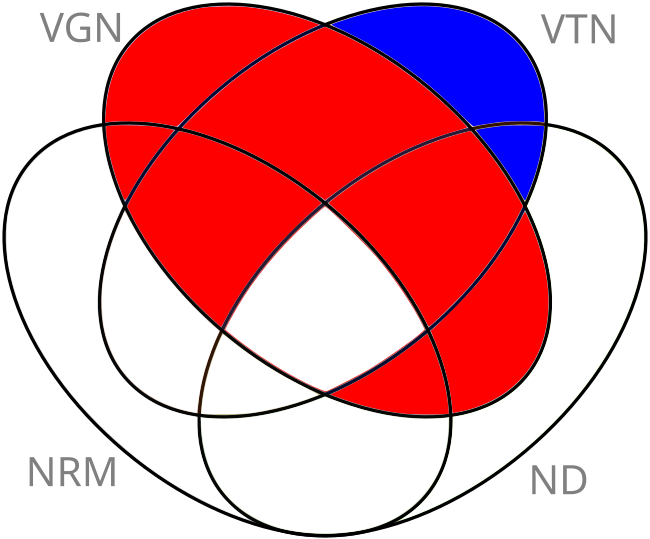
Bu diyagramdaki renkleri ve harfleri açıklayalım:

VGN “vegan”, VTN “vejetaryen”, NRM “kırmızı et yok”, ve ND “süt ürünü yok” anlamına geliyor.
Kırmızı bölgeler imkansız çünkü “vegan” diğer üç parametreyi beraberinde getiriyor.
Mavi bölgeler de imkansız çünkü bir yiyecek hem kırmızı et içerip hem de vejetaryen olamaz. Mavi bölgeler “kırmızı et yok"un dışında ama “vejetaryen"in içinde. Aslında iki bölgeyi daha mavi renkle boyayabilirdik ama onlar önceden kırmızıya boyandığı için gerek duymadım.

İmkansız olan bölgeleri kesinleştirdiğimize göre Venn diyagramını biraz basitleştirelim:

Diyagramdaki sayılar, partide hangi kategoride kaç dolma olduğunu gösteriyor.

İki kategorinin ("$0$” ve “$\underline{0}$” ile işaretli) dolma partisinde olmadığını görüyoruz. Bunların hala mümkün olduğunu göstermek için bu kategorilere girecek dolma örnekleri vermemiz gerekiyor:

$0$: Yumurta ve/veya bal içeren ama hiçbir et veya süt ürünü içermeyen bir dolma. Hiç bu kategoride bir dolma görmedim (ya da yemedim – bir dolmayı görmeden de yiyebilirsiniz…). Bu biraz garip bir kombinasyon ayrıca. Ama mesele bunun mantıklı değil, mümkün olması.
$\underline{0}$: Tavuk eti içeren ama kırmızı et veya süt ürünü içermeyen bir dolma.

Şu ana kadar yaptıklarımızı özetleyelim. $2^4 = 16$ kombinasyon arasında sadece $7$‘sinin mümkün olduğunu bulduk. Sonra her kategoride kaç dolma olduğunu saydık. 23. dolma partisinde görülmeyen kategoriler için de o kategorilere girecek dolma örnekleri verdik. Bu son kısmı gelecekteki dolma partileri için bir öneri olarak görmeyin, gördürmeyin.

Şimdi yukarıdaki Venn diyagramlarını çizerken dikkatimi çeken bir durumu ele alalım.

Daha dengeli bir dağılım için yeni kategoriler

Dolmaların kategorilere dağılımının dengesiz olduğunu gözlemliyoruz. Bazı kategorilerde çok dolma var, bazı kategorilerde ise hiç dolma yok. Bu bize şu soruyu sorduruyor:

“Dolmaları aralarında daha eşit dağıtacak başka kategoriler var mı?”

Önce birkaç detayı netleştirmemiz gerek. Parti sırasında iki aşamalı bir süreç vardı: Önce dört parametre tanımlandı, sonra da bu dört parametrenin her olası kombinasyonuna “kategori” denildi. Burada ise kategorileri doğrudan tanımlayacağız.

Yiyeceklerimizi malzeme varlığı/yokluğu ile tanımlanmış ikili vektörler olarak modelleyelim:

	Sığır eti	Tavuk eti	Domates	Zeytinyağı	Süt	Tereyağı	Bal
Yiyecek 1	1	0	1	0	1	0	1
Yiyecek 2	0	1	1	0	0	1	1
Yiyecek 3	1	1	0	1	0	0	1
Yiyecek 4	0	0	1	1	1	0	0
Yiyecek 5	1	0	0	1	0	1	0

Yani “kategori” sözcüğünü, hangi malzemelere izin verildiğini/verilmediğini belirten bir Boolean ifade olarak tanımlayabiliriz. Venn diyagramındaki bölgeler nasıl kesişmiyorsa kategorilerin de kesişmesine izin vermeyeceğiz. Bu kural nedeniyle “vegan”, “vejetaryen”, “kırmızı et yok” ve “süt ürünü yok"u kategori değil, parametre olarak adlandırdık önceki paragraflarda.

Yukarıdaki tabloyu esas alırsak partideki dört parametrenin tanımları şöyle oluyor:

Kırmızı et yok = "sığır eti" YOK
Süt ürünü yok = "süt" YOK VE "tereyağı" YOK
Vejetaryen = "sığır eti" YOK VE "tavuk eti" YOK
Vegan = "sığır eti" YOK VE "tavuk eti" YOK VE "süt" YOK VE "tereyağı" YOK VE "bal" YOK

Elimizdeki veride başka malzemeler olsaydı tabi ki farklı tanımlara ihtiyacımız olurdu. Örneğin yiyeceklerden bazılarında yumurta olsaydı “vegan"ın tanımına "yumurta" YOK ifadesini eklememiz gerekirdi.

Dolmaları sınıflandırmak için kullandığımız dört parametrenin mantıklı olduğununun altını çizeyim. Bunlar bazı insanların gerçek hayatta uyduğu kurallar. Dolmaları birbirleri arasında daha dengeli dağıtan kategoriler ararken bu kategorilerin günlük hayatta anlamlı olup olmadığını umursamayacağız.

Doğrusal programlama kullanacağız. Önce algoritmamızın girdilerini netleştirelim. Dolmaları kaç kategoriye böleceğimiz bize söyleniyor. Ayrıca her dolmanın hangi malzemeleri içerdiğini biliyoruz, dolayısıyla partide (tüm dolmaları toplarsak) hangi malzemelerin kullanıldığını da biliyoruz. Bunları biraz daha matematiksel olarak ifade edelim:

$m$: yiyecek sayısı
$d$: malzeme sayısı
$n$: kategori sayısı
İkili matris $M \in \{0,1\}^{m \times d}$: Eğer $j$ yiyeceği $k$ malzemesini içeriyorsa $M_{j,k} = 1$, içermiyorsa $M_{j,k} = 0$.

Algoritmanın görevi:

Her yiyeceği birbirini dışlayan $n$ kategoriye dağıtmak
Her kategoriyi malzeme varlığını/yokluğunu belirten Boolean kurallarla tanımlamak
En büyük ve en küçük kategori arasındaki boyut farkını olabildiğince azaltmak (kategori boyutlarındaki dengesizliği tanımlamanın başka yolları da var)

Değişkenler:

$x_{i, j} \in \{0, 1\}$: $j$ yiyeceği $i$ kategorisine atandı.
$p_{i, k} \in \{0, 1\}$: $i$ kategorisinin kurallarında $k$ malzemesinin bulunma zorunluluğu var.
$a_{i, k} \in \{0, 1\}$: $i$ kategorisinin kurallarında $k$ malzemesinin bulunmama zorunluluğu var.
$r_{i, j, k} \in \{0, 1\}$: $j$ yiyeceği $i$ kategorisindeki $k$ malzemesi hakkındaki kurala uyuyor.
$r_{i, j} \in \{0, 1\}$: $j$ yiyeceği $i$ kategorisinin tüm kurallarına uyuyor.
$S_{\text{max}}, S_{\text{min}} \in \mathbb{Z}_{\geq 0}$: en büyük ve en küçük kategorilerin boyutları.

Amaç fonksiyonu: $$ \begin{aligned} \min(S_{\text{max}} - S_{\text{min}}) \end{aligned} $$

Kısıtlamalar:

Atama kuralı: Her yiyecek tam olarak bir kategoriye atanmalı (ne daha az ne de daha fazla). $$ \begin{aligned} \sum_{i = 1}^n x_{i, j} = 1 \ \ \ \ \forall j \in \{ 1, \dots, m \} \end{aligned} $$
Bir yiyecek bir kategoriye atandıysa o kategorinin tüm şartlarını karşılıyor olmak zorunda: $j$ yiyeceği sadece her $k$ malzemesi için varlık/yokluk koşullarıyla tanımlanan kuralı karşılıyorsa $i$ kategorisine atanabilir: $$ \begin{aligned} x_{i, j} \leq (1 - p_{i, k}) (1 - M_{j, k}) + (1 - a_{i, k}) M_{j, k} \ \ \ \ \forall i,j,k \end{aligned} $$ Açıklama:
- $M_{j, k} = 0$ ise elimizde $x_{i, j} \leq 1 - p_{i, k}$ kalıyor.
- $M_{j, k} = 1$ ise elimizde $x_{i, j} \leq 1 - a_{i, k}$ kalıyor.
Bir yiyecek bir kategorinin tüm şartlarını karşılıyorsa o kategoriye atanmak zorunda: Bu diğerlerinden biraz daha karmaşık olacak.
- Önce kurala uyuluyorsa $r_{i, j, k} = 1$ olmasını sağlayacağız:
  - $M_{j, k} = 0$ ise (yani malzeme yiyecekte yoksa): $$ \begin{aligned} r_{i,j,k} \leq 1 - p_{i, k} \ \ \ \ \forall i, k \end{aligned} $$ $$ \begin{aligned} r_{i,j,k} \geq a_{i, k} \ \ \ \ \forall i, k \end{aligned} $$ İlk eşitsizlik, malzeme olmak zorundaysa “kurala uyuyor” olarak kaydetmememizi garantiliyor. İkinci eşitsizlik, malzeme olmamak zorundaysa “kurala uyuyor” olarak kaydetmemizi garantiliyor.
  - $M_{j, k} = 1$ ise (yani malzeme yiyecekte varsa): $$ \begin{aligned} r_{i,j,k} \leq 1 - a_{i, k} \ \ \ \ \forall i, k \end{aligned} $$ $$ \begin{aligned} r_{i,j,k} \geq p_{i, k} \ \ \ \ \forall i, k \end{aligned} $$ İlk eşitsizlik, malzeme olmamak zorundaysa “kurala uyuyor” olarak kaydetmememizi garantiliyor. İkinci eşitsizlik, malzeme olmak zorundaysa “kurala uyuyor” olarak kaydetmemizi garantiliyor.
  - O malzeme için herhangi bir kural yoksa “kurala uyuyor” olarak kaydediyoruz: $$ \begin{aligned} r_{i,j,k} \geq 1 - p_{i, k} - a_{i, k} \end{aligned} $$
- $j$ yiyeceği $i$ kategorisinin tüm kurallarına uyuyorsa $r_{i, j} = 1$: $$ \begin{aligned} r_{i,j} \geq \left( \sum_k r_{i,j,k} \right) - (d - 1) \ \ \ \ \forall i,j \end{aligned} $$
- $r_{i, j} = 1$ ise $j$ yiyeceğinin $i$ kategorisine atanmasını garantileyelim: $$ \begin{aligned} x_{i,j} \geq r_{i,j} \end{aligned} $$
Çelişmeyen malzeme koşulları: Bir kategori bir malzemenin hem olmasını hem de olmamasını zorunlu kılamaz. $$ \begin{aligned} p_{i, k} + a_{i, k} \leq 1 \ \ \ \ \forall i, k \end{aligned} $$
Kategori boyutlarının ilgili değişkenlere bağlanması: $S_{\text{max}}$ ve $S_{\text{min}}$‘i temsil etmeleri gereken şeyleri temsil etmeye zorluyoruz. $s_i = \sum_{j = 1}^m x_{i, j}$ tanımını yapalım (yani $s_i$ = $i$ kategorisindeki yiyecek sayısı). O zaman $$ \begin{aligned} s_i \leq S_{\text{max}} \ \ \ \ \forall i \end{aligned} $$ ve $$ \begin{aligned} s_i \geq S_{\text{min}} \ \ \ \ \forall i. \end{aligned} $$

Algoritmanın kodu

Bu problem için Python temelli bir kütüphane olan PuLP kullanılarak yazılmış bir kodu burada bulabilirsiniz. Kodun içinde boyutları bir dolma partisini temsil etmeye yetecek boyutlarda (30 yemek, 30 malzeme) rastgele bir matris de var.

Algoritmaya kodun içindeki 30’a 30’luk matristeki yiyecekleri 5 kategoriye böldürdüğünüzde bu sonucu veriyor:

Result - Optimal solution found

Objective value:                0.00000000
Enumerated nodes:               2121
Total iterations:               113678
Time (CPU seconds):             21.71
Time (Wallclock seconds):       21.77

Option for printingOptions changed from normal to all
Total time (CPU seconds):       21.73   (Wallclock seconds):       21.80

Objective (S_max - S_min): 0.0

Category 0:
  Food 0
  Food 3
  Food 4
  Food 13
  Food 16
  Food 18
  Rule:
    NOT Ingredient 0
    NOT Ingredient 1
    HAS Ingredient 3
    HAS Ingredient 27

Category 1:
  Food 1
  Food 6
  Food 7
  Food 11
  Food 21
  Food 24
  Rule:
    HAS Ingredient 8
    HAS Ingredient 20
    HAS Ingredient 21
    NOT Ingredient 23

Category 2:
  Food 2
  Food 17
  Food 19
  Food 20
  Food 26
  Food 27
  Rule:
    HAS Ingredient 0
    HAS Ingredient 7
    HAS Ingredient 18
    HAS Ingredient 23

Category 3:
  Food 5
  Food 9
  Food 12
  Food 22
  Food 28
  Food 29
  Rule:
    HAS Ingredient 1
    HAS Ingredient 3
    NOT Ingredient 7

Category 4:
  Food 8
  Food 10
  Food 14
  Food 15
  Food 23
  Food 25
  Rule:
    NOT Ingredient 3
    NOT Ingredient 18

Sonuç

Programın 30’a 30’luk matris için çalışma süresi dizüstü bilgisayarımda yaklaşık 22 saniyeydi. Bu süre pek uzun değil ama parametreleri biraz bile arttırmak çok daha uzun çalışma sürelerine yol açıyor (doğrusal programlama için bu çok şaşırtıcı değil). Bu tip problemlerde buluşsal yöntemler mantıklı olabiliyor.

Kaynakça

Venn diyagramı buradan alındı. Değişiklik yapıldı.
Doğrusal programlamlama kısmındaki desteklerinden ötürü Claude ve ChatGPT’ye teşekkür ediyorum. Verdikleri birkaç tavsiye sayesinde işleri daha hızlı bitirdim. Problemi hangi yolla çözmemin daha mantıklı olduğuna karar verirken de onların fikirlerini göz önünde bulundurdum.
Kodun çoğunluğunu yapay zeka yazdı. Ben denklemlere son şeklini verdikten sonra Claude/ChatGPT’den PuLP kullanarak by denklemlere denk gelen bir kod yazmasını istedim. Yapay zeka sayesinde insanlık basit ama meşakkatli işlerle daha az zaman kaybediyor, bu sayede zor işlere daha çok zaman ayırabiliyor.