Dolma Party

[Türkçe] [code]
[Substack]

I recently attended the 23rd edition of an annual dolma-themed dinner party. As you can imagine, this has become a tradition for some people – I was just two years old when the first one took place. Everyone was required to bring a homemade dolma. A “homemade” dolma bought from a supermarket didn’t count: “your dolma must be homemade by your hands,” per an official email from the organizers. I spent a nontrivial amount of time preparing my contribution to the party, so hopefully cooking dolma builds character or something.

I helped out with the registration process during the party. Newcomers would receive a label for their dolma before placing it at the dining area. Importantly, this label contained dietary information in the form of four parameters: “vegan,” “vegetarian,” “no red meat,” and “no dairy.” This blog post is about some observations and thinking on this dietary information.

First, we observe that not all $2^4 = 16$ combinations are possible here. “Vegan” implies the rest, so there cannot be a dolma that contains red meat, but is vegan at the same time. If someone manages to make such a dolma, that would be a hell of an achievement. So, which combinations are valid? First, we will lay down all possible combinations. Then, for each combination, we will either argue that it is impossible or list some ingredients that a dolma can/must have in order to satisfy that combination. To aid with this, I drew the following Venn diagram:

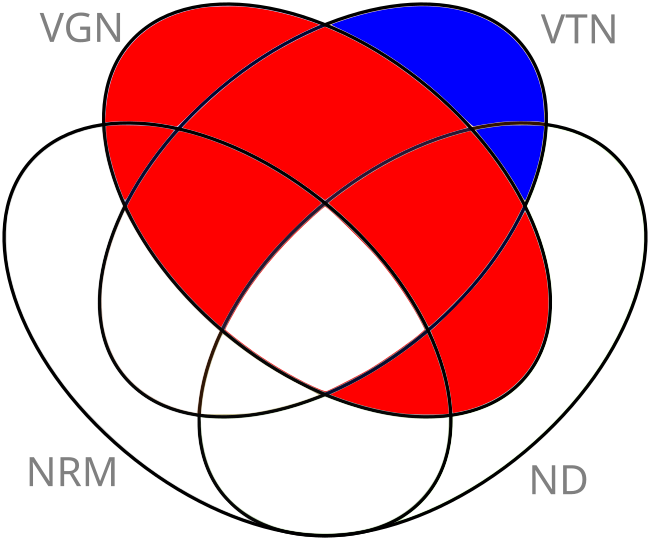
Let’s go through the various colors and letters on this diagram:

VGN stands for “vegan,” VTN stands for “vegetarian,” NRM stands for “no red meat,” and ND stands for “no dairy.”
The red regions are impossible because “vegan” implies the other three parameters.
The blue regions are also impossible because a food cannot contain red meat and be vegetarian at the same time. The blue regions are outside of “no red meat” but within “vegetarian.” Note that there are two other regions that we could have colored blue, but they were already colored red.

Now that we know that certain regions are impossible, let’s simplify the Venn diagram:

The numbers denote how many dolmas there were in each category.

Note that two categories (marked with “$0$” and “$\underline{0}$”) were not seen at the dolma party. To show why they are still possible, we need to give examples of dolmas that would be in these categories:

$0$: A dolma with eggs and/or honey, but no kind of meat or dairy. This is a silly combination, I have never seen (or eaten – one can eat a dolma without seeing it…) a dolma in this category. But the point is that this is possible.
$\underline{0}$: A dolma with chicken but no red meat or dairy.

To conclude this part, we found that among $2^4 = 16$ combinations, only $7$ of them are possible. Then, we counted how many dolmas are in each category. For categories that did not appear in the 23rd dolma party, we gave examples of ingredient combinations that can be used to make dolmas in those categories. This last bit should not be seen as a suggestion for future dolma parties.

The next step is to address a situation that piqued my interest while drawing the Venn diagrams above.

New categories for a more homogeneous distribution

We observe that the distribution of dolmas among the categories is skewed: a lot of dolmas accumulated in certain categories, while some categories had no dolmas. This brings us to the following question:

“Are there other categories that would have distributed the dolmas more equally among each other?”

We need to explain/clarify a few things first. During the party, there was technically a two-step process: first, four parameters were defined, and second, each possible combination of these four parameters was called a “category.” In this analysis, we will define the categories directly.

Let’s model foods as binary vectors over ingredient presence:

	Beef	Chicken meat	Tomato	Olive oil	Milk	Butter	Honey
Food 1	1	0	1	0	1	0	1
Food 2	0	1	1	0	0	1	1
Food 3	1	1	0	1	0	0	1
Food 4	0	0	1	1	1	0	0
Food 5	1	0	0	1	0	1	0

In this setting, a category is a Boolean expression that describes which ingredients are allowed/not allowed. Importantly, we won’t allow categories to intersect, just like how the regions in the Venn diagrams were not intersecting. It is because of this rule that we called “vegan,” “vegetarian,” “no red meat” and “no dairy” not as categories, but as parameters.

For the table above, we have the following definitions for the four parameters at the party:

No red meat = NOT "beef"
No dairy = NOT "milk" AND NOT "butter"
Vegetarian = NOT "beef" AND NOT "chicken meat"
Vegan = NOT "beef" AND NOT "chicken meat" AND NOT "milk" AND NOT "butter" AND NOT "honey"

Of course, if we had other ingredients in our input data, we would need different definitions. For example, in another input where eggs are an ingredient in a food, we would have to add NOT "egg" to the definition of “vegan.”

Note that the four parameters that we used to classify the dolmas made sense – these are actual dietary restrictions some people follow. While looking for categories that split the dolmas more equally among each other, we will not care if these categories are meaningful from a culinary perspective. We are done with macadamia, now is the time for academia.

We will use linear programming. Let’s first clarify what our algorithm will receive as input. We are given how many categories we are supposed to split the dolmas into. We also know the ingredients of each dolma. As an implication, we also know which ingredients were used for the entire party. In more technical terms, here is our input data:

$m$: number of foods
$d$: number of ingredients
$n$: number of categories
A binary matrix $M \in \{0,1\}^{m \times d}$ where $M_{j,k} = 1$ if food $j$ contains ingredient $k$

The goal:

Assign each food to exactly one of $n$ mutually exclusive categories
Define each category by a Boolean rule over ingredient presence/absence
Minimize the size difference between the largest and smallest category (note: there are other ways to define imbalance in category sizes)

The variables:

$x_{i, j} \in \{0, 1\}$: food $j$ is assigned to category $i$.
$p_{i, k} \in \{0, 1\}$: ingredient $k$ must be present in category $i$.
$a_{i, k} \in \{0, 1\}$: ingredient $k$ must be absent in category $i$.
$r_{i, j, k} \in \{0, 1\}$: food $j$ satisfies rule in category $i$ about ingredient $k$.
$r_{i, j} \in \{0, 1\}$: food $j$ satisfies all rules of category $i$.
$S_{\text{max}}, S_{\text{min}} \in \mathbb{Z}_{\geq 0}$: the maximum and minimum category sizes.

Objective function: $$ \begin{aligned} \min(S_{\text{max}} - S_{\text{min}}) \end{aligned} $$

Constraints:

Exclusive assignment: each food must be assigned to exactly one category. $$ \begin{aligned} \sum_{i = 1}^n x_{i, j} = 1 \ \ \ \ \forall j \in \{ 1, \dots, m \} \end{aligned} $$
If a food is assigned to a category, it must satisfy all rules of that category: food $j$ can only be assigned to category $i$ if it satisfies the rule defined by presence/absence conditions for each ingredient $k$. $$ \begin{aligned} x_{i, j} \leq (1 - p_{i, k}) (1 - M_{j, k}) + (1 - a_{i, k}) M_{j, k} \ \ \ \ \forall i,j,k \end{aligned} $$ Explanation:
- if $M_{j, k} = 0$, the term becomes $x_{i, j} \leq 1 - p_{i, k}$.
- if $M_{j, k} = 1$, the term becomes $x_{i, j} \leq 1 - a_{i, k}$.
If a food satisfies all the rules of a category, it must be assigned to that category: this one will be a bit more complicated than the others.
- First, we’ll ensure that $r_{i, j, k} = 1$ if the rule is satisfied:
  - if $M_{j, k} = 0$ (if the ingredient isn’t present in the food): $$ \begin{aligned} r_{i,j,k} \leq 1 - p_{i, k} \ \ \ \ \forall i, k \end{aligned} $$ $$ \begin{aligned} r_{i,j,k} \geq a_{i, k} \ \ \ \ \forall i, k \end{aligned} $$ The first inequality ensures that if presence is required, we do not record as “follows the rule.” The second inequality ensures that if absence is required, we record as “follows the rule.”
  - if $M_{j, k} = 1$ (if the ingredient is present in the food): $$ \begin{aligned} r_{i,j,k} \leq 1 - a_{i, k} \ \ \ \ \forall i, k \end{aligned} $$ $$ \begin{aligned} r_{i,j,k} \geq p_{i, k} \ \ \ \ \forall i, k \end{aligned} $$ The first inequality ensures that if absence is required, we do not record as “follows the rule.” The second inequality ensures that if presence is required, we record as “follows the rule.”
  - if there are no rules for that ingredient, record as “follows the rule”: $$ \begin{aligned} r_{i,j,k} \geq 1 - p_{i, k} - a_{i, k} \end{aligned} $$
- If food $j$ satisfies the requirement of category $i$ about all ingredients, then $r_{i, j} = 1$: $$ \begin{aligned} r_{i,j} \geq \left( \sum_k r_{i,j,k} \right) - (d - 1) \ \ \ \ \forall i,j \end{aligned} $$
- Finally, if $r_{i, j} = 1$, then food $j$ must be assigned to category $i$: $$ \begin{aligned} x_{i,j} \geq r_{i,j} \end{aligned} $$
Non-conflicting ingredient conditions: a category cannot require both the presence and the absence of the same ingredient. $$ \begin{aligned} p_{i, k} + a_{i, k} \leq 1 \ \ \ \ \forall i, k \end{aligned} $$
Link category sizes to the relevant variables: force $S_{\text{max}}$ and $S_{\text{min}}$ to represent what they are supposed to. Let $s_i = \sum_{j = 1}^m x_{i, j}$ be the number of foods in category $i$. Then $$ \begin{aligned} s_i \leq S_{\text{max}} \ \ \ \ \forall i \end{aligned} $$ and $$ \begin{aligned} s_i \geq S_{\text{min}} \ \ \ \ \forall i. \end{aligned} $$

Running the algorithm

Here is an implementation of the constraint system above using PuLP in Python. The code comes with a uniformly-sampled matrix representing 30 foods and 30 ingredients, the dimensions of which were meant to roughly represent a dolma party.

For the readers to get a sense of the output of the algorithm, below is what you get when you tell the algorithm to split the foods in the 30 foods by 30 ingredients matrix (the one provided in the code) into 5 categories:

Result - Optimal solution found

Objective value:                0.00000000
Enumerated nodes:               2121
Total iterations:               113678
Time (CPU seconds):             21.71
Time (Wallclock seconds):       21.77

Option for printingOptions changed from normal to all
Total time (CPU seconds):       21.73   (Wallclock seconds):       21.80

Objective (S_max - S_min): 0.0

Category 0:
  Food 0
  Food 3
  Food 4
  Food 13
  Food 16
  Food 18
  Rule:
    NOT Ingredient 0
    NOT Ingredient 1
    HAS Ingredient 3
    HAS Ingredient 27

Category 1:
  Food 1
  Food 6
  Food 7
  Food 11
  Food 21
  Food 24
  Rule:
    HAS Ingredient 8
    HAS Ingredient 20
    HAS Ingredient 21
    NOT Ingredient 23

Category 2:
  Food 2
  Food 17
  Food 19
  Food 20
  Food 26
  Food 27
  Rule:
    HAS Ingredient 0
    HAS Ingredient 7
    HAS Ingredient 18
    HAS Ingredient 23

Category 3:
  Food 5
  Food 9
  Food 12
  Food 22
  Food 28
  Food 29
  Rule:
    HAS Ingredient 1
    HAS Ingredient 3
    NOT Ingredient 7

Category 4:
  Food 8
  Food 10
  Food 14
  Food 15
  Food 23
  Food 25
  Rule:
    NOT Ingredient 3
    NOT Ingredient 18

Conclusion

For the 30 by 30 matrix, the runtime was around 22 seconds on my laptop. While this runtime is acceptable, increasing the parameters even slightly leads to much longer runtimes, which is not that surprising for linear programming. A next step could be to explore some heuristics – the current algorithm looks for the optimal solution.

Acknowledgements

Venn diagram of four ellipses with all 15 possible intersections by RupertMillard, taken from here. Changes were made.
Thanks to Claude and ChatGPT for making my life easier in the linear programming part. They did give me a few good suggestions, which saved me time. I also considered their opinions when deciding which strategy to pursue to solve the problem.
The code was mostly generated by AI, and has my stamp of approval. Once I finalized the equations, I asked Claude/ChatGPT to generate PuLP code representing them. Thanks to AI, we humans have more time to work on hard tasks because we now spend less time with easier but tedious tasks.